Maximum entropy solver for the “Wordle” problem.

If you don’t know what Wordle is, take a quick break to familiarize yourself over at https://www.powerlanguage.co.uk/wordle/.

If you just want to see the solver itself, see the link at the bottom of the page.

This simple and elegantly designed game captures just the right amount of randomness with strategy, making it an addictive pandemic-era hobby, with a neat backstory. In this word-guessing game, feedback is given on the basis of the identity and locations of letters in each guessed word, making it an elimination problem to identify the correct word. This game is very similar to the game Mastermind but with words.

The rules are simple, if the player guesses a letter correctly, in the correct position, it is marked green. If the player guesses a letter correctly in the incorrect position, it is marked yellow. If the player guesses an incorrect letter (or exceeds the number of times the letter appears in the word), it is marked grey. Players have six turns to identify the “secret” word.

Alright so what? The game actually presents an interesting computational challenge. Can a player always pick the right combination of words in order to win the game in six turns or less? From a cursory check of Twitter, there are dozens of people who have developed or are developing their own solvers for this game.

Wordle basically uses a Scrabble dictionary as a basis for the words the user can guess. However, the developers decided that many of the words are too obscure (e.g. VOZHD) for use as answers in the game, and thus use a reduced letter set of 2315 words which are simple enough to be in the common lexicon.

Disappointingly, this reduced word list from which the answer may be drawn is available in the source code, and it appears that the game simply iterates over the list in ordered fashion, making it possible to immediately see which word will be selected the next day. :( While this doesn’t ruin the game really, it’s better to protect things that are not supposed to be known by a player in order to keep the game fun even for those who are curious enough to look at the source code. It’s the same reason magicians use curtains - without them the magic is gone.

Source-code cheating aside, the computational challenge still stands - how would you pick words so that you maximize your chances of winning the game?

One of the more basic strategies is to make picks based on (positional) letter frequencies - e.g. start with AROSE or similar words which contain a combination of the most frequent letters in all five letter words. This may get a user pretty far, but struggles on certain words which contain more infrequently used letters of the alphabet. The approach also struggles to reduce wordsets that are highly similar, such as

WATER
HATER
LATER
MATER
RATER

etc…

A second strategy is to guess words which eliminate as many words as possible on each guess. There are multiple ways to accomplish this, one naive approach is to look at which words have any overlap with other words, and pick ones that so that overlap and non-overlap words are separated as equally as possible, a la binary search.

This idea is in theory quite good. A more refined version of this idea goes as follows. Instead of a binary overlap/no overlap strategy, what if the method attempts to maximize the entropy of the possible ways clues could be returned from the guess?

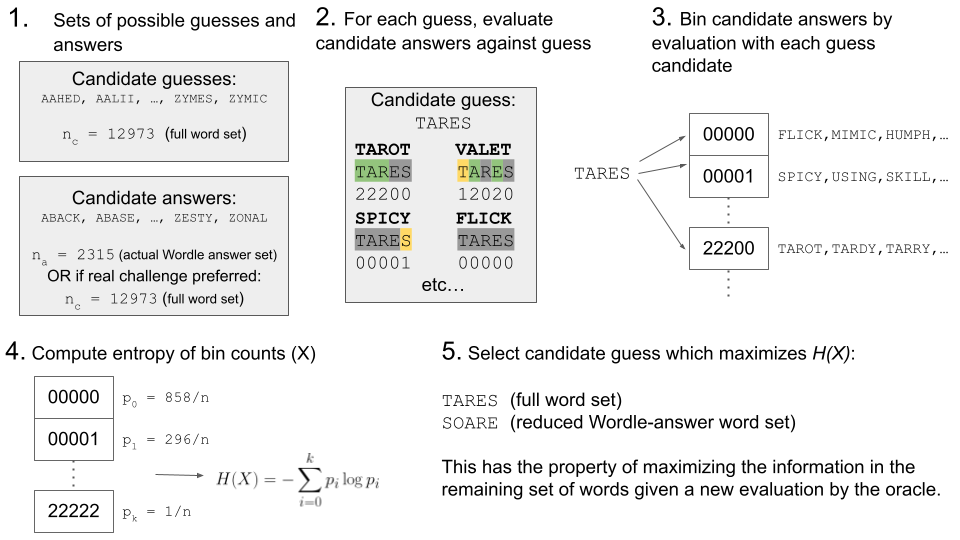
That is, for a given guess and a set of candidate words which may be the answer based on prior feedback, evaluate the possible set of feedbacks that can occur for the possible guess. This results in a collection of different feedback strings, between the possible guess and each of the candidates, e.g. 10010 or 22001 or 00000, etc. The entropy is computed on the number of candidates assigned to each bin for the current candidate guess. The best guess maximized the entropy in order to give the greatest chance of reducing the candidate set by as much as possible. This way, for any feedback that is returned by Wordle (the “oracle”), then the probability that the remaining set of words is as small as possible is maximized. If the bins did not have maximum entropy (words not spread as evenly as possible), then a random feedback would be more likely to land on a larger bin than a smaller one, and thus would not eliminate as many words as possible given the feedback.

A diagram of how the method works is shown below:

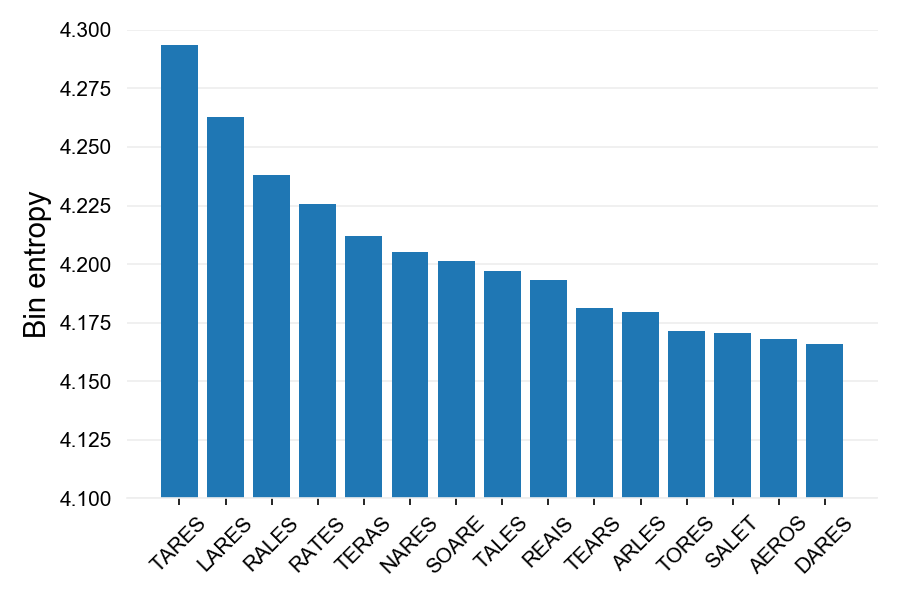
Here’s what the entropy distribution looks like for the top 15 hits in the full Wordle set. I found the maximum-entropy initial word for default Wordle is SOARE while for expanded wordlists it is TARES.

Ties introduced by this maximum entropy method can be resolved with a few heuristics.

1. Check the non-overlap bin 00000 and pick the guess which minimizes its size.
2. Pick a guess which is also a candidate (important when remaining set very small and few guesses left)
3. Maximize the entropy of the letters in the guess.
4. Consider the positional frequencies of the guess letters in the remaining possible answers and maximizes the total positional frequency.

So, how well does this strategy perform?

On the default Wordle answer set, the strategy always guesses the correct answer within six turns (100% win rate), and uses the starting word SOARE. However since the Wordle developers only use a reduced answer-space to make the game easier, how well does it do if the possible answer can be any of the 12927 words in the Wordle dictionary? How about for the Scrabble five letter words? In those two cases, this strategy gets 99.67% and 99.71% of the words correct, respectively within six turns when we start with TARES.

One of the most revealing things about this method is that sometimes when the player is getting close to having an answer, it is better to take a step back to a guess which uses fewer correct letters, but which reduces the remaining search space by a larger amount. For instance, in our WATER example, if one knew -ATER, then the maximum entropy answer actually backs off and picks something like ELCHI, which eliminates EATER, LATER, CATER and HATER all in one go!

There is also a fun variation of this, where the game is “evil” and picks a different word after you make your guess, making it as hard as possible to get the right answer. This version is actually extraordinarily fun and I recommend checking out one implementation of it here.

WordleSolver

Here is a link to the web-app which runs this method.

The source-code for the solver is also available here: https://github.com/jluebeck/WordleSolver

Acknowledgments:

I’d like to thank Ben Pullman for good discussions about this problem.